文章地址：https://www.computer.org/csdl/proceedings-article/sp/2019/666000a294/13HFz28TNuP
标题：PrivKV: Key-Value Data Collection with Local Differential Privacy
作者：Qingqing Ye, Haibo Hu, Xiaofeng Meng, Huadi Zheng
发表会议：S&P 2019

Abstract

Local differential privacy (LDP), where each user perturbs her data locally before sending to an untrusted data collector, is a new and promising technique for privacy-preserving distributed data collection. The advantage of LDP is to enable the collector to obtain accurate statistical estimation on sensitive user data (e.g., location and app usage) without accessing them. However, existing work on LDP is limited to simple data types, such as categorical, numerical, and set-valued data. To the best of our knowledge, there is no existing LDP work on key-value data, which is an extremely popular NoSQL data model and the generalized form of set-valued and numerical data. In this paper, we study this problem of frequency and mean estimation on key-value data by first designing a baseline approach PrivKV within the same “perturbation-calibration” paradigm as existing LDP techniques. To address the poor estimation accuracy due to the clueless perturbation of users, we then propose two iter- ative solutions PrivKV M and PrivKV M+ that can gradually improve the estimation results through a series of iterations. An optimization strategy is also presented to reduce network latency and increase estimation accuracy by introducing virtual iterations in the collector side without user involvement. We verify the correctness and effectiveness of these solutions through theoretical analysis and extensive experimental results.

Introduction

当前已经有很多工作做过频率估计（直方图估计）和均值估计了，但是对于KV类型的数据，却没有相关的工作，对于$< Key, Value >$的数据，我们想统计key的频率和对应key的均值，如果仅仅把现在已有的用在这一套上面，是会出现问题的。比如假定数据是:

$\{<Cancer, 0.6>, <HIV, 0.9>, <Fever, 0.08>\}$

如果把Cancer直接替换成Fever的话，对应的值也需要改到对应的空间中，不然就会导致均值估计存在问题了，不然数据就会变得没有意义。所以作者提出了基于LDP的Key-Value数据的收集及频率估计和直方图估计方法。

根据作者的描述，这篇文章有这么几个贡献点：

形式化了privacy-preserving key-value data数据的收集和分析（均值估计和直方图估计）问题，并且设计了很好Local perturbation protocol (LPP) 用来perturbate。
设计了三个保证$\epsilon$-DP的LPP方法，分别是 $PrivKV$ , $ PrivKVM$ 和 $PrivKVM^+$。
设计了适用于data collector的优化机制，包含虚拟优化（即不需要用户参与的迭代）。

第三点可能现在还不太容易理解，我们先慢慢来看。

这部分我就不说了，大概介绍了一下现在和频率估计，均值估计什么的一些相关工作。

Preliminaries and Problem Definition

Random Response

之前提到过很多次的是对于二元值，Random Response就是以一定概率翻转回答，以一定概率不翻转回答，不翻转回答概率为：

$p = \frac{e^\epsilon}{e^\epsilon+1}$

我们看一下对于binary data，比如只有 0 和 1，用户那里1的频率为$a$，则报告的1的比例为多少呢？

$a' = a \cdot p+ (1-a) \cdot (1-p) = (2p-1)a + 1-p$

所以有 $a = \frac{a’+p-1}{2p-1}$，也就是说，原始比例和匿名数据比例之间有一个映射关系，即假如匿名数据下统计的结果为 $f$ 的话，那么原始数据的结果为：

$f'=\frac{p-1+f}{2p-1}$

问题定义

我们先把符号说明一下：

Symbol	Description
$\mathcal{U}$	用户的集合
$n$	用户的数量，$n = \mathcal{U}$
$u_i$	$\mathcal{U}$ 中的第$i$个用户
$\mathcal{K}$	key的集合
$d$	key的数量，$d=\mathcal{K}$
$S_i$	$u_i$的KV对
$l_i$	$S_i$中KV对的数量，$l_i = S_i$
$< k_j, v_j >$	$S_i$中第$j$个KV对
$f_k$	键$k$的频率
$m_k$	键$k$对应的value的均值

首先我们试想一下场景，首先由$n$个用户，这些用户放在一起就是$\mathcal{U}$，即$\mathcal{U}=\{u_1, u_2, …, u_n\}$，然后有一系列键，$\mathcal{K}=\{1,2,…,d\}$，为了方便我们这里暂且用阿拉伯数字表示键，每个键对应的值呢，我们假定分布在$\mathcal{V}=[-1,1]$中。然后第 $i$ 个用户她有 $l_i$ 个键值对 $S_i = \{ < k_j, v_j > |1 \le j \le l_i; k_j \in \mathcal{K}; v_j \in \mathcal{V} \}$。然后我们希望这些数据发给不可信的数据收集者之后，数据收集者可以统计出一下每个键的频率和每个键对应的值的均值：

Frequencey estimation: 即统计用户中有多少用户拥有这个键： $f_k = \frac{ \lvert \{ u_i \lvert \exists < k , v > \in S_i \} \rvert }{n}$
dMean estimation：即统计出这个键对应的值的均值 $m_k = \frac{\sum_i \sum_{j:k_j=k} v_j}{n\cdot f_k}$

其实还有一个假定，就是每个用户同一个键只能出现一次。

PrivKV: A baseline approach

A Flawed Key Perturbation Protocol

首先我们需要把用户的KV对映射成一个定长的KV对，按照一下这个方法：

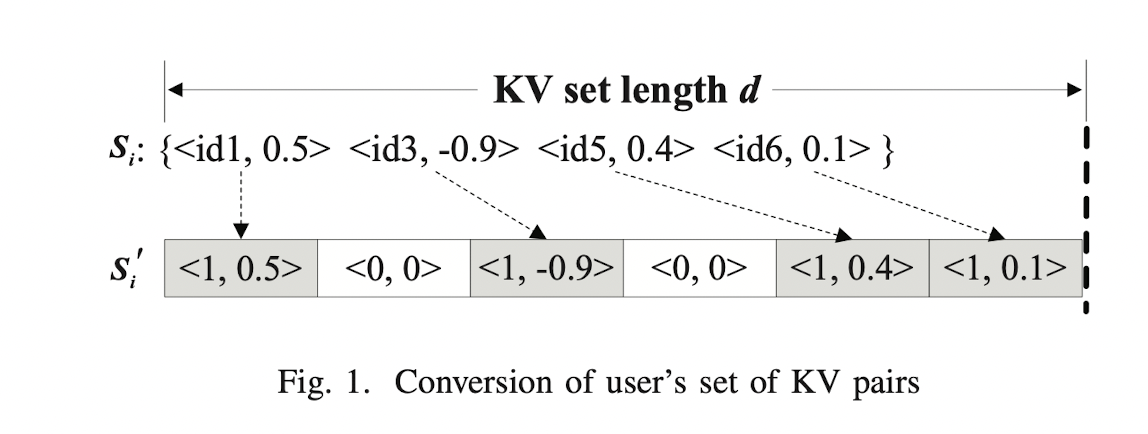
也就是说，对于 id 的话，你有，就是 1，没有就是 0。然后对于值的话，有 id 就保留原来的值，没有 id 值就是0。当然，这里需要注意，我们得先把键按照一定顺序排序好。因为一共的K值有 $d$ 个，所以每个人的KV对就变成了一个 $d$ 维的二元组了。我们说对于第$i$个二元组$ < k_i, v_i > $，如果 $k_i=1$，那这个键就是存在的，等于0就是这个键不存在的。然后我们现在在这个 $d$ 维的二元组上面做手脚。

要保护隐私，所以不能老老实实把自己的KV报告上去，要做一个perturbate处理，既然要perturbate，那么我们现在就有以下几种变化的可能性了：

$1\rightarrow 1$，即存在$\rightarrow$存在：这种情况下这个键值对保持不变，即$ < 1, v > \rightarrow < 1, v > $。
$1\rightarrow0 $，即存在$\rightarrow$不存在：这种情况下说明原来的键不存在，但是现在键存在了，我们直接将键对应的值设为0即可，即$ < 1, v > \rightarrow < 0, 0 > $。
$0\rightarrow 0$，即不存在$\rightarrow$不存在：这种情况下原来不存在的键值对，现在还是不存在，即$ < 0, 0 > \rightarrow < 0, 0 > $。
$0\rightarrow 1$，即不存在$\rightarrow$存在：本来不存在的键值对突然变得存在了，这个时候，给值随便从 $[-1,1]$ 定一个就好。

Local Perturbation Protocol: A Remedy

接下来我们来看，那些存在不存在的，去变。这里提到了两个算法，我先来介绍一下，首先是Harmony的算法，如下图：

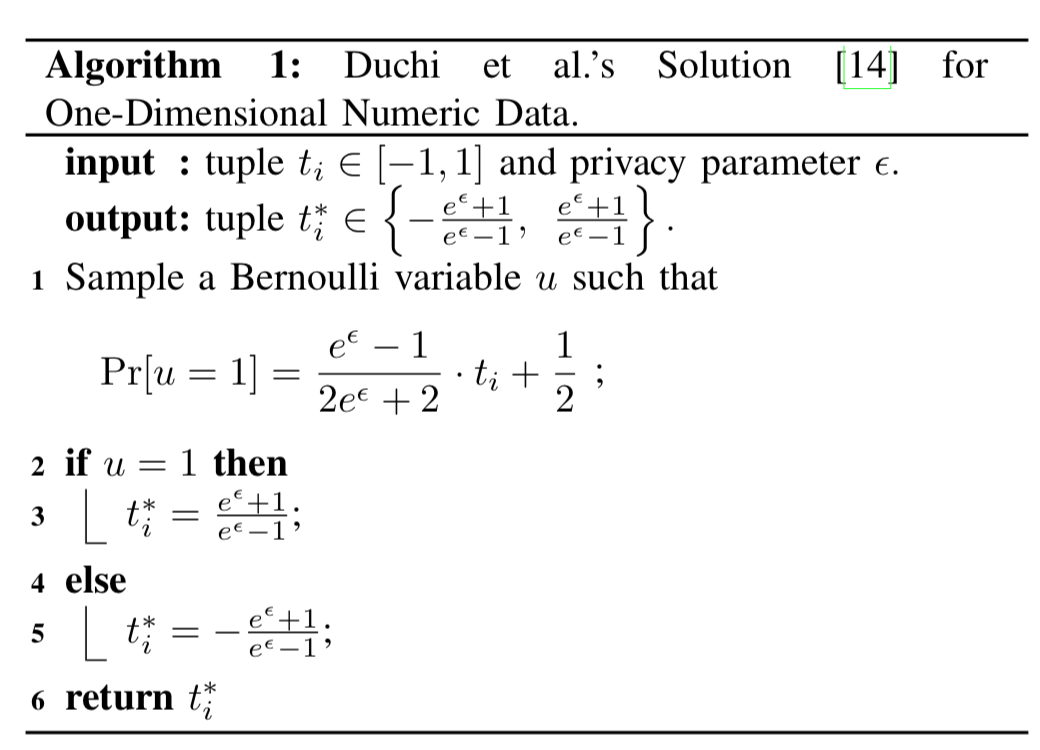
fig-alg01

这一类算法实际上在Random Response里面我们都见过，这个算法是说我们可以对数据进行均值估计，注意算法的第5行乘了一个$d$，这纯粹是因为第2行对$d$维数据进行了一个随机采样的过程，说起来起到了压缩传输数据的作用，毕竟原来需要发送$d$个01比特，现在只用发送一个了。不过这带来了估计的误差，要想使得达到原有的精度，说不动原来只要10000个人的数据，现在需要$10000\cdot d$ 个人才行。只是噱头。所以这个算法就over了。

fig-alg02

然后再看这里的Value Perturbation Primitive算法，实际上没啥区别，还是用来做均值估计的，而且这个估计的均值和原始的均值之间是一个线性关系，不像Harmony算法那样用$\frac{e^\epsilon+1}{e^\epsilon-1}$进行了一个校正。

当然多说一句，其实我们之前多次提到过，满足均值估计的一定是概率上的线性变化，比如这里的Discretization就是把概率空间变到$[0,1]$，然后Perturbation就是把$[0,1]$的概率空间压缩到$[\frac{1}{e^\epsilon+1}, \frac{e^\epsilon}{e^\epsilon+1}]$，实际上这两部完全可以直接用一步去表示，即把原始数据映射到概率空间$[\frac{1}{e^\epsilon+1}, \frac{e^\epsilon}{e^\epsilon+1}]$中。当然，分开写更容易理解了。

再多说一句，这里文中说Harmony的方法不好，因为Harmony中有个$d$，采样的过程可能导致偏差，但是算法3给的实际上就是算法2中$d=1$的情况，构不成Harmony方法不好的理由。而且这个Value Perturbation Primitive还没有对估计的均值进行校正（当然后面还是会校正的）。

fig-alg03

好了，现在我们可以看这个LPP算法了，我们来分析一下这个过程，首先第2行进行了一个采样，从$d$个KV对中选了一个，就像前面说的一样，采样只是说起来压缩了网络传输的带宽而已，至少说起来是个优点了，采样就不看了。这时候就有两种情况了，要么这个键原来是1，即原来存在，要么这个键原来是0，即原来不存在。为了能做频率估计，我们只要用这个0还是1去做映射就好了。

如果K是存在的那么第四行对V进行了一个perturbation操作，perturbation依然可以做均值估计的。如果K不存在则随机产生一个V然后对V做perturbation操作。所以对V均值估计的时候有两个方面，首先需要估计出K存在的比例，在根据这个比例估计出V的均值。

从DP的角度来看，$\epsilon$ 分成了两个部分，一部分用来对V处理（$\epsilon_2$），一部分用来对K处理（$\epsilon_1$），很容易证明，这个算法是满足$\epsilon$的。

接下来问题就成了怎么去基于LPP算法的结果估计频率和均值了。

我们先来看K的频率估计，算法的第5行和第9行说，我们以$p= e^\epsilon / (e^\epsilon+1)$的比例真实回答这个K是不是真的存在，所以根据我们前面Random Response里面介绍的校正，我们统计出收到的结果中1的比例（假设为$f_k^*$），然后就可以估计出原始数据的1的比例，即估计的Key的频率为：

$f_k = \frac{p-1+f_k^*}{2p-1}$

对于K，我们现在有N个数据，假如原始数据中有x个是1，y个是-1吧，所以原始数据的均值为：

$M_{mean} = \frac{x-y}{N}$

那么收到的数据中，假如1的个数为A，-1的个数为B，则我们有：

$\begin{align} & A = x \cdot p + y \cdot (1-p) = y + p(x-y) \nonumber\\ & B = y \cdot p + x \cdot (1-p) = x + p(y-x) \nonumber\\ \end{align}$

其中，$p = \frac{e^{\epsilon_2}}{e^{\epsilon_2}+1}$ 因此两个式子相减我们就有：

$B-A = (y-x) - 2p(y-x)=(1-2p)\cdot N \cdot M_{mean}$

所以估计的均值为：

$M_{mean} = \frac{B-A}{(1-2p) \cdot N}$

接下来就可以看这个算法4了，也是一个完整的含有用户端和收集端的算法了，实际上就是在说收集者收集了这个数据之后该怎么去估计均值和频率。

fig-alg04

算法4中的第6行即频率估计，然后第11行的公式，就是我们用AB给出的均值估计的结果了。

讲到这里，如果不算一下的话，感觉还挺对的，实际上，这里的均值估计是存在比较大的问题的，如果估计的是所有数据的均值，那么这个公式是没有问题的，但是我们需要计算的是key中的value的均值，所以这里实际上是引入了比较大的误差的。作者也意识到了这个问题，接下来作者就带我们来消除这个误差。

$PrivKVM$: An Interative Solution

An Interative Model

我们先来设想一个场景。假如我们现在能做到均值估计了，估计的均值为 $m$，那么对于所有的$ < 1 , v > $ 的数据，我们就可以认为其全部都是 $ < 1, m > $ 了，然后相当于现在只有两种数据，即有值的是$ < 1, m > $，没值的是$ < 0, 0 > $，所以我们想在这个情况下把 $m$ 给算出来。

直接想的话，我们不是那么容易算出来（先不管能不能算出来吧，反正不是那么容易算出来）。那这个时候怎么办呢，重新想一想，如果没值的不是$ < 0, 0 > $，而是$< 0 , m > $ 的话，我们不就可以直接把统计到的结果一拿，算出来的值就是$m$了。这种假设之下，有两个优点：

对于 $< 1, v >$ 的数据，虽然有一部分变成了$< 0, 0 > $但是只统计key=1的记录不影响均值。
对于 $<0>$ 的数据，变成1的部分均值为$m$，所以统计的均值还是为m。

基于上面的这两个优点，只需要在收到的数据之中统计 $< 1, v > $ 的数据然后计算的均值就可以认为是原始数据的均值了。对吧，又简单又暴力。

但是这里有个矛盾：要想这个方法work，就需要提前知道m，要想知道m，就需要这个方法work。

看上去这个问题好想解决不了了，没事，有误差不要紧，我们慢慢消除误差，所以作者提出了基于迭代的方法。我们先来看看怎么个迭代：

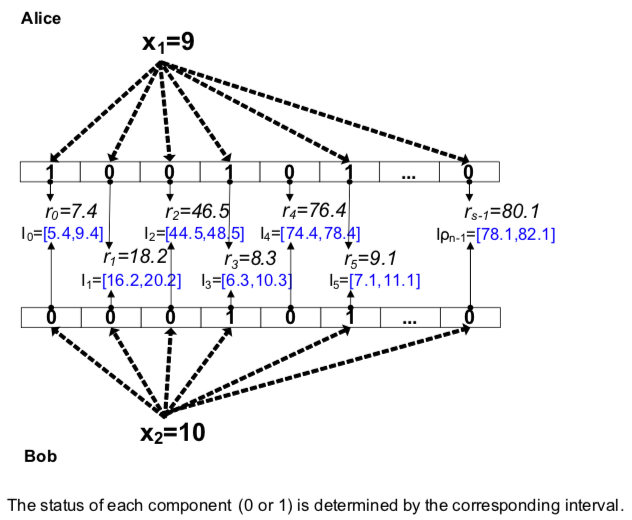
fig02

上面的6235就是迭代的过程，也就是说，对于没有key的用户，还是先按照以往的思路随机产生一个数据。但是，然后根据估计的结果需要计算一个当前轮的均值，然后，下一轮就不重新产生数据了，而是把当前轮的均值传递给没有key的用户，让他用这个值表示他的值。理解上来看，这样随着一直估计下去，每次估计的值就会越来越接近均值了。

细心的同学这时候就会想到了，均值估计的任务算是解决了，那么隐私保护程度你这么一直算下去会爆炸啊。确实是这样子的，一轮下来是 $\epsilon$，$n$ 轮下来就是 $n\cdot \epsilon$了，真的是计算一时爽，一直计算一直爽啊。也正因此，需要有个Privacy Budget Allocation策略了，简称PBA策略。过程也简单粗暴，假如你要算 $c$ 轮，那么我给每轮的预算就是 $\epsilon / c$，所以每一轮的参数为 $\epsilon_1 = \epsilon_2 = \frac{\epsilon}{2c}$。

文中的定理5.1花了比较大的篇幅去证明，核心思想就是如果Collector返回的是估计的均值，那么基于这个均值对所有原始数据的估计就可以估计出key对应的均值，并且这个估计是无偏估计。按照我的分析思路下去的话是比较好证明的，作者的证明过程我就忽略了这里。

$PrivKVM$

可能由于我读论文没那么细吧，我没看到作者为什么把这个机制名字叫 PrivKVM，个人猜测是因为多了个均值 $m$ 的返回过程，所以这里用了字母 $m$。不过作者在解释算法的时候用的是 PrivKVM: Iterative PrivKV，哈哈，要是我的话这个算法名字可能就叫做 I-PrivKV了。

fig-alg05

算法5就是PrivKVM算法了。了解了迭代的过程之后，这个算法也就懂了。反正就是迭代，再迭代。

至于文字部分，也说了这个算法还可以干别的事，读起来感觉很自然。但是要我自己写，我也写不出来这些玩意，可见写论文还是很需要功底的，读的时候自然可以读懂核心方法，可是写的时候还得面面俱到才行。

Privacy and Accuracy Analysis

这一章节分析了隐私和准确性吧，隐私方面说了$PrivKVM$满足$\epsilon$-DP，这个也没啥好说的。不过，I doubt it! 暂且不在这里分析了。

定理5.3说如果无限轮进行下去的话，即 $c \rightarrow \infty$，那么估计的均值的期望就等于实际的均值。理解上来看的话，就是每一轮误差都在减小，一直估计就一直小了。

定理5.4作者说证明过程类似参考文献，由于之前我已经用过chernoff bound了，这个公式看上去很像chernoff bound，虽然我也不确定是不是，这里也就没有继续深究了。

$PrivKVM^{+}$: An Adaptive Variant

作者说，如果$PrivKVM$要估计的比较准确的话，$c$怎么取很麻烦，讲道理$c$越大理论上的估计会越准，但是$c$太大会造成现实生活中的通信开销或者要求更多次的计算执行时间等，所以作者又提出了一个自适应的$PrivKVM^{+}$算法。

所以对于第 $r$ 迭代，我们定义一个开销函数，其中包含两部分开销 $F_1(r)$ 表示准确率开销（accuracy cost），$F_2(r)$ 表示通信开销（communication cost），所以总的开销可以表示为 $F(r) = F_1(r) + F_2(r)$。我们先看一下，准确率开销怎么算，作者采用了Absolute error，即：

$F_1(r) = \frac{1}{d} \sum_{k\in \mathcal{K}}|m_k - m_k^{(r)}|$

对于通信开销，由于每次开销都是常数，假设为$A_0$吧，所以通信开销为：

$F_2(r) = A_0 \cdot r$

所以这里的开销并不是指第 $r$ 轮的开销，而应该理解为前 $r$ 轮一共的开销。然后作者分析了一下，随着 $r$ 增大，根据定理5.3的分析这个准确率开销应该是越来越大的，而通信开销在常数增加，所以$F_r$是可以达到全局最小的，我们只要找到这个$r$就好了：

$F(r)-F(r-1)=A_0 - \frac{1}{d}\sum_{k\in \mathcal{K}}|m_k^{(r)}-m_k^{(r-1)}|$

作者这里说假定第$r$轮计算的均值比第$r-1$轮更接近理想的均值，所以我们就可以达到全局最优了，这时候就不用继续往下算了。这里我就有点不解了，从期望的角度来看第$r$轮比第$r-1$轮准确，但是不应该把期望上的直接认为单次也是这样啊。

fig-alg06

算法6就展示了这个过程的一个流程，这里的$PBA_t$采用了exponential decay的策略来分配budget，即每次分掉剩余的$1/t$作为当前的$\epsilon$。

其实我不太明白这个代码的好处在哪里，作者提出这个代码是为了使得准确率尽量高的前提下尽可能地减少计算代价。这些在期望的情况下都是比较理想的，但是由于有离散化的过程（discretization和perturbation都会引入离散化），我觉得单词的误差会比较大，特别是在当前轮$\epsilon$很小的情况下。那么问题就比较大了，万一你第一轮的计算结果算出个$F^*$小于0，按照这个算法就不往下算了，这还是比较不科学的。究其原因，就是因为作者假定了$|m_k-m_k^{(r)}| < |m_k-m_k^{(r+1)}|$，而这只是统计意义上如此。

Virtual Iterations: An Optimization on Latency and Accuracy

到目前为止，$privKVM$算法感觉还是很不错的，但是呢，其需要每次计算出均值然后让用户再来根据我计算的均值回馈，然后迭代计算。这样用户很累啊。作者说，我就只要从用户那里收集一次数据，后面的 $c-1$ 轮迭代，我都可以自己完成，这里成为虚拟迭代（Virtual Iterations），听上去amazing啊。话不多说，摆出算法先（算法7）：

因为用户只要参与一次计算，所以$\epsilon_1 = \epsilon_2 = \epsilon / 2$。所以频率第一次就可以估计出来了，然后也可以估计出第一轮的均值，这个过程前两行就完成了。

定理6.1给定了参数，并说明了执行 $c$ 轮迭代之后计算出的均值，回想一下定理5.3说无限轮迭代之后得到的均值就是真实的均值，但是是基于反馈-迭代的过程的，这里的机制当中去掉了反馈的过程，为什么还可以用定理5.3中的证明过程来当做结论呢，这里我觉得有点问题（毕竟都没有反馈了，怎么优化？）。

好了，读到这里我就没明白作者的表达意图了，首先第一轮的估计就不是无偏的，那么你基于第一轮的估计结果，怎么估计也都是有偏的啊。如果这样，多次迭代的目的是什么呢。

Experimental Evaluation

这部分，真的好长啊。

先来看一下实验当中的几种方法：对于key的频率估计，采用了RAPPOR, k-RR 和 SHist，对于均值估计，作者将算法2替换成了 Harmony 和 MeanEst 算法，然后用 PrivKVM，所以这两个方法就叫做PrivKVM-Harmony和PrivKVM-MeanEst，然后再和文中提到的PrivKVM对比。

再来看一下数据集，数据集这里面用的还是比较多的，这里就不细说了，可以看这个表，其中前三个是生成的数据，第一个服从指数分布，第二个服从幂律分布，第三个服从线性分布。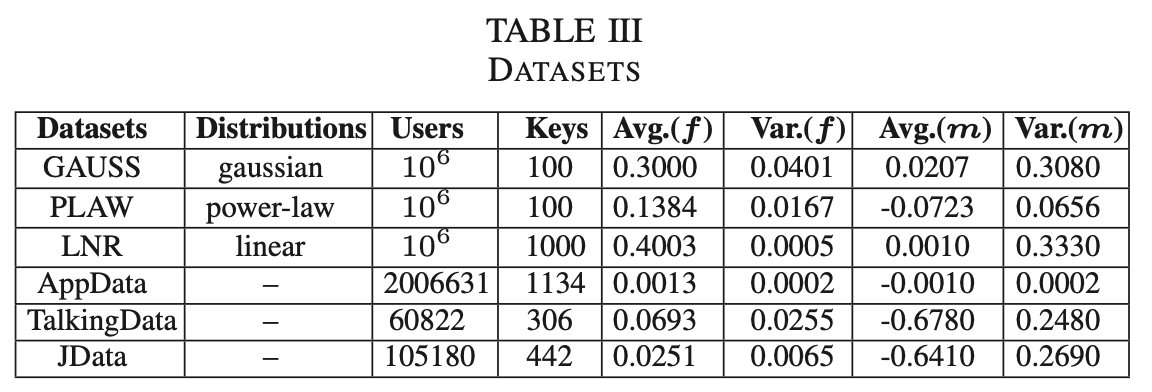
table03

然后是对于误差的分析，这里采用了以下两个误差：

Relative Error (ER): 就是我们正常说的相对误差。与之对应的还有一个绝对误差，绝对误差就是估计值和真实值的差的绝对值，相对误差就要再除以一个真实值，看的是相对于真实值的误差比例。
$RE = Stat_{k\in \mathcal{K}}\frac{ \lvert f_k - f_k^* \rvert}{f_k}$
这里的$Stat$函数指的是一种统计的方程，比如对于$k$的平均误差，或者最高的$10\%$的误差。
Mean Square Error (MSE): 就是正常说的平方误差，有为有那么多个key，所有求一个平均平方误差。
$MSE = \frac{1}{d} \sum_{k\in \mathcal{K}}(m_k - m_k^*)^2$
作者这里说他们用的平方误差取了个对数，可能是太大了，图片上面放不下吧。

Overall Results

fig03

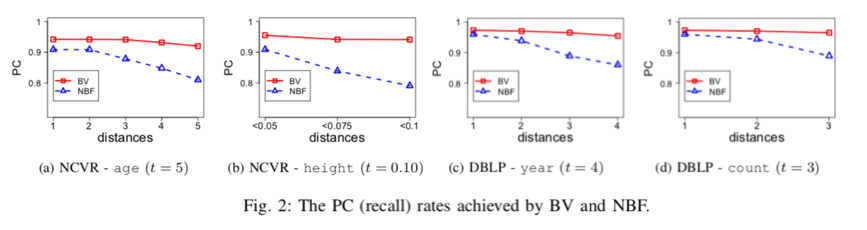
图3说了总体的误差，说明PrivKVM效果还是不错的。尤其是$\epsilon$很小的时候效果不错。

图4是频率估计的结果，总的来说，饰演的效果笔其他几个方法的效果都要好。

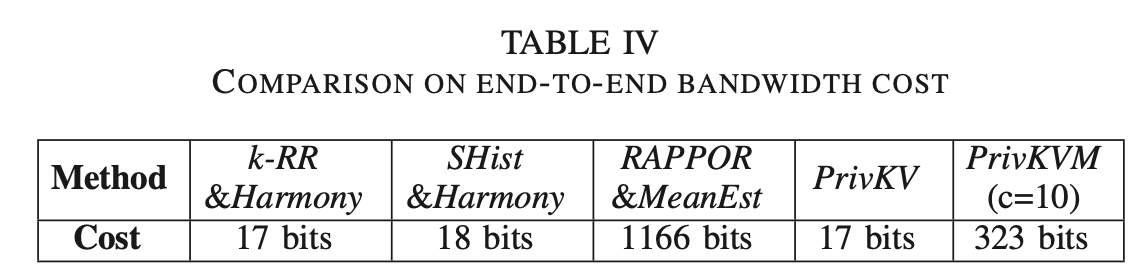
table04

上表给出了不同方法需要传输数据的大小。AppData上面一共有1134个Keys，这里我就不知道为什么用了1166bits了，如果说每个用户拥有多个key的话，rappor完全也可以执行采样的操作的。

Scalability

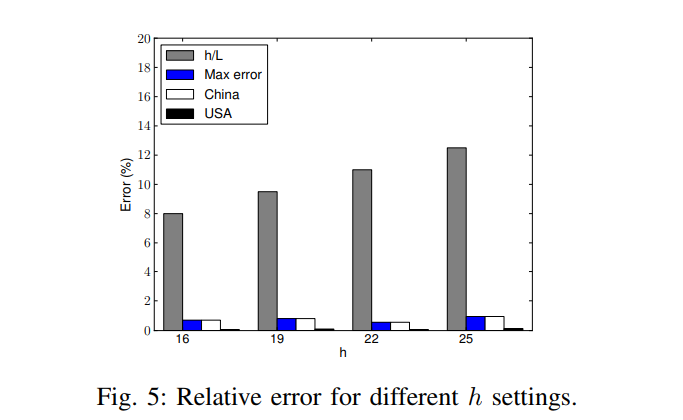
fig05

scalability说的是用户数量和key的数量对数据估计的影响，虽然大家都知道对于同一个方法数据越多越准确，但是同样的数据下，你的方法比别人准确就是你厉害了。图5展示了不同用户数量下的误差。

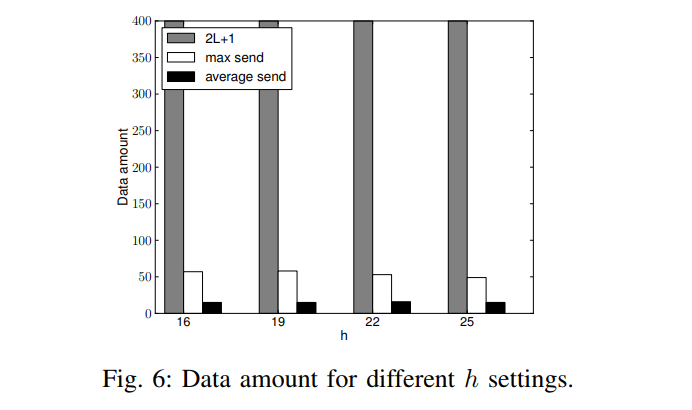
fig06

图6展示了不同key数量下各种方法的误差。

Key-value Correlation

fig07

这里提到了一个KV关联的实验，采用了Pearson correlation coefficient，中文名叫皮尔森相关系数。我目前还不知道这个实验怎么做的，从实验结果上来看，PrivKVM这个方法随着epsilon的增大，会更接近实际上的相关系数。

fig08

在图8中，展示了高斯分布数据下，不同epsilon下均值估计的效果，我们可以看出来的是，当keyid很小和很大时，误差比较大。根据这个实验和高斯分布这两个东西，我猜测作者生成数据时越是靠中间的数据越多，并且均值越大。所以才会出现两端误差较大的情况，因为数据量较小。对比来说，其他的方法就比较差了。（不过我感觉这个实验说到底也就是均值估计，其他的方法不至于这么差吧。）

Impact of Iterations

图9展示了不同迭代次数对实验效果的影响，差不多就是迭代次数越高，误差越小。

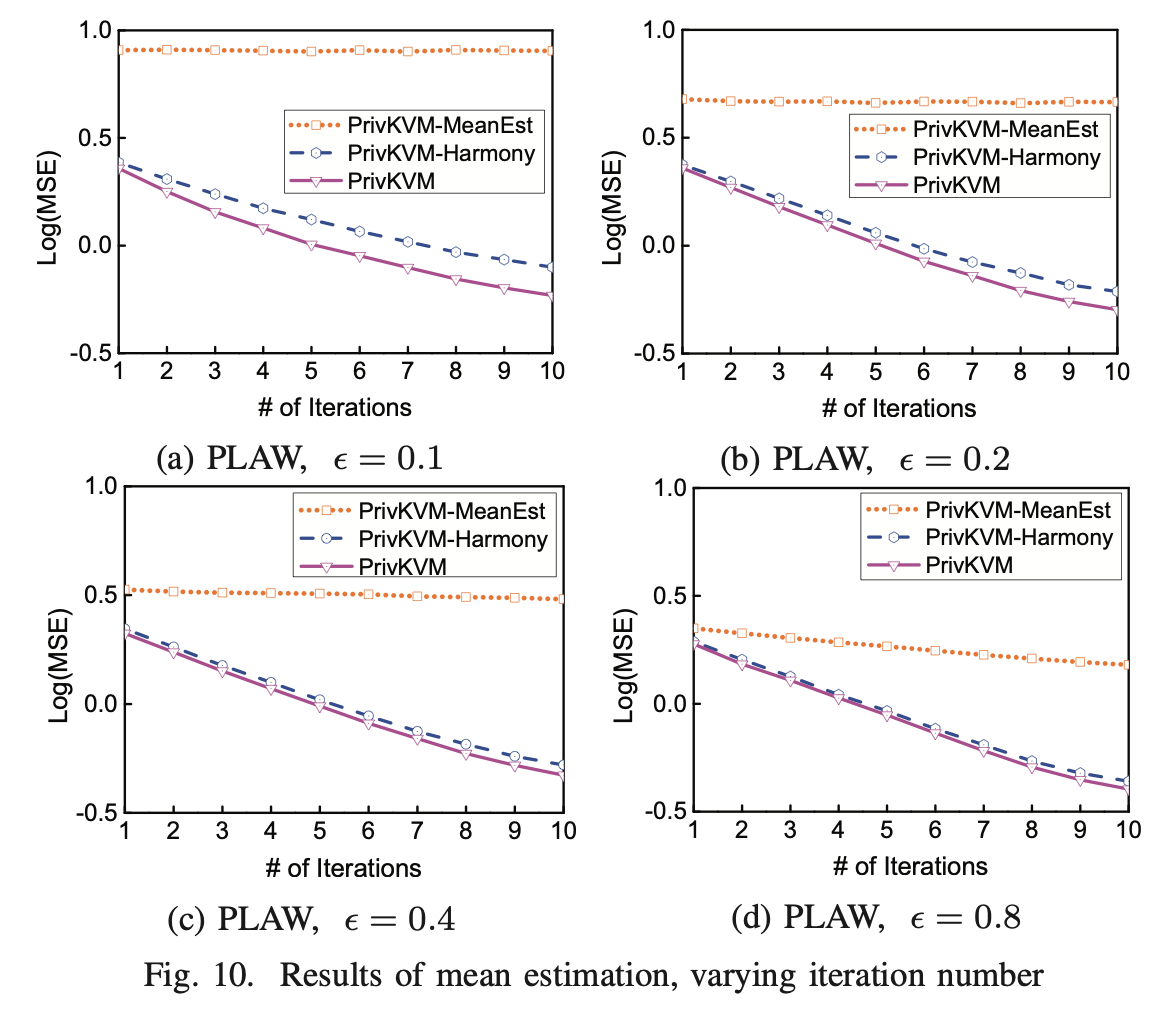
fig10

图10就是比较不同方法了，和图9实验类似。

Impact of Cost Function

fig11

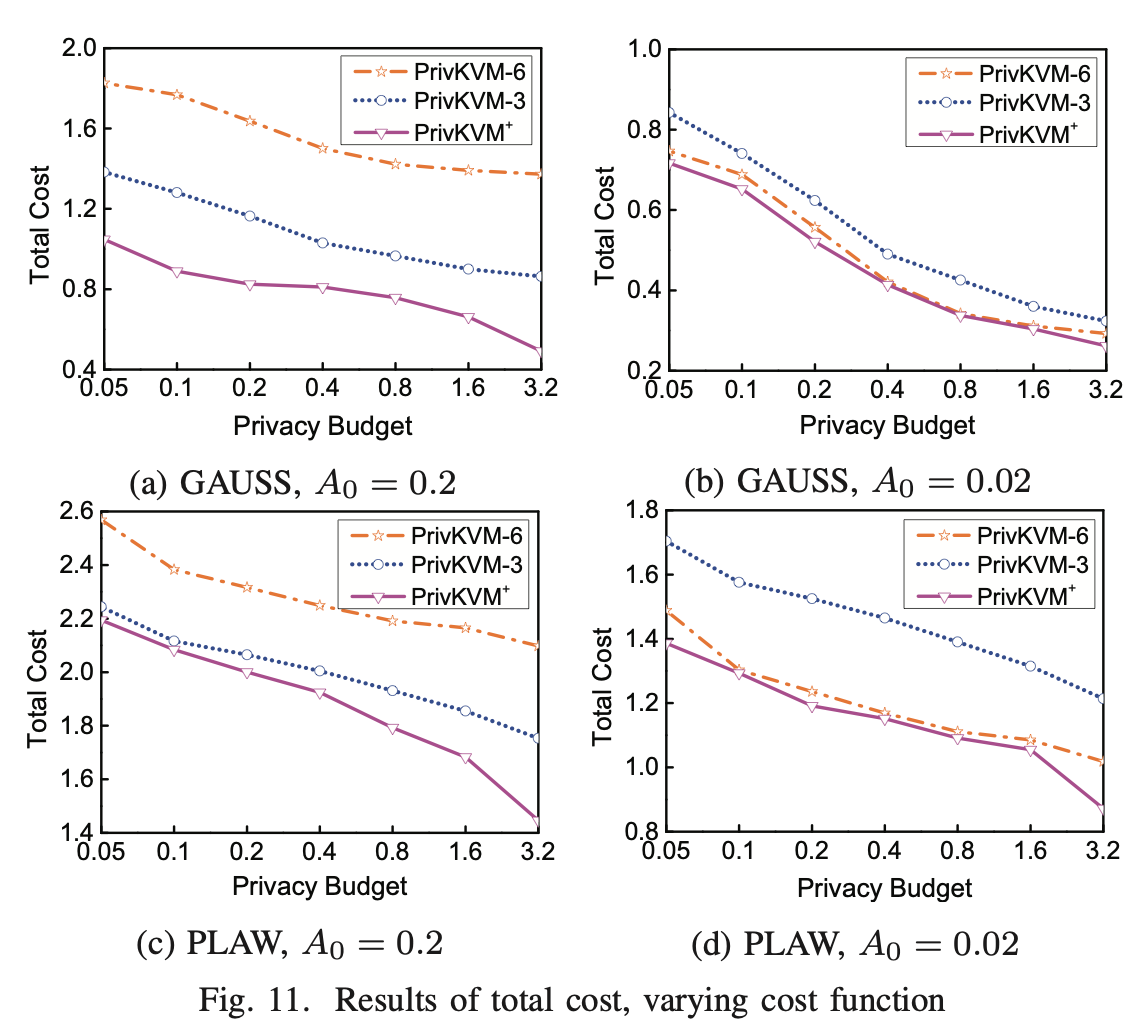
这里好玩了，作者没有比较估计的误差，而是用Cost来衡量，因为还有通信误差，得出的结论是，我们这样的总体cost很小。

Impace of Virtual Iteration Optimization

图12说的是运用了虚拟迭代的实验，将$PrivKVM$不用迭代和用迭代来对均值进行估计，从实验结果上来看，只要 $\epsilon$ 不是特别小，用了迭代之后估计的更准确。

Conclusion

总结就是本文提出了对于KV数据的频率估计和均值估计方法，提出了三种方法，以及优化方法~还讲了以后想要做的事情，至于这个是不是能做成，还不一定。毕竟基于二元估计的目前也就只能估计个均值出来，梯度什么的就别想了。

我的总结

读了这篇文章，受益匪浅。主要由以下几个疑问还没有解决：

PrivKVM尝试利用迭代的方法去使得估计的值更接近真实的均值，这个出发点是很好的。作者也证明了这是一个无偏估计。无偏估计意味着理论上的均值估计结果等于均值。但是，我们以$c=10$即10轮估计为例，第九轮的均值估计结果是要经过一个离散化的操作的，比如是实际均值为0.9，第九轮估计的结果也为0.9，那离散化的过程一不小心离散化成-1了，这第十轮的误差就可能很大了。毕竟无偏估计是期望上的无偏估计。因为饰演的结果作者没有用箱体图表示，所以现在也不能确定这个方法一定很好，毕竟没有看到最大误差。
$privKVM$ 中的$\epsilon$ 问题，I doubt it. 我会再分析。
算法$PrivKVM^{+}$的有效性我有待怀疑，在文中已经分析过了。
Lemma 6.2证明过程用到了定理5.3，这个问题在文中已经说过了。

我列出了一些疑问，对于其中的任意一个疑问，如果你可以回答我，欢迎联系我和我讨论，我可以请喝奶茶，谢谢。

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。

《差分隐私》